State of Charge: SOC is related to the stored energy in the battery and defined as the ratio of charge extract from the cell at a specific point in time to the total capacity. It is measured in terms of percentage. If the battery is fully charged, SOC of the battery is said to be 100%. An estimate of SOC is an important input to balancing, energy, and power calculations of the battery pack. It is calculated as

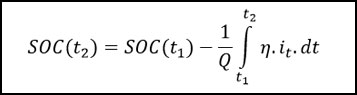
Where SOC (t2) - SOC at time t2, SOC (t1) - SOC at time t1 , η-Coulombic efficiency, i_t – Charge/Discharge current at time t and Q – Full capacity

In Discrete form

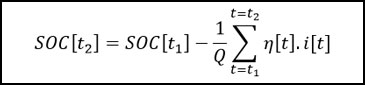
SOC is something similar to a dashboard fuel gauge that reports a value from “Empty” (0 %) to “Full” (100 %). But, measuring SOC accurately is more challengeable as compare to Fuel gauge measurement. There are a lot of sensors available to measure a gasoline level in a tank accurately, but presently no direct sensor is available to measure SOC of the battery pack.

SOC Estimation Methods

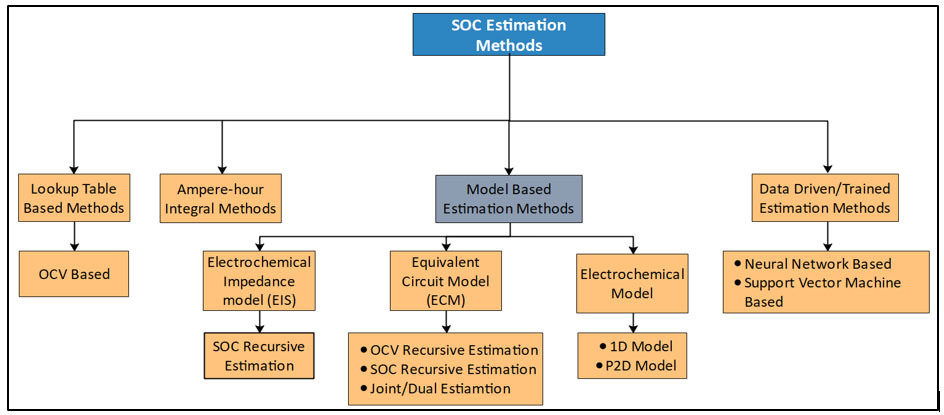
Figure 2 shows different SOC estimation methods.

Advantages of an Accurate SOC Estimation

Performance: With good SOC estimation, performance of the battery pack will be enhanced. With known error bounds, one can aggressively use the battery pack capacity.

Longevity: An accurate SOC estimation may prevent cells to damage by not overcharge/over-discharge the battery pack.

Compactness: Accurate SOC and battery state information allows the battery pack to be used aggressively within the design limits

Reliability: A good SOC estimator is consistent and enhancing overall power-system reliability.

Economy: Warranty service on a reliable system costs less.

Exicom's Role

R&D Exicom is aggressively working on SOX (SOC, SOH, SOP and SOE) algorithms with novel research.
For SOC estimation, Exicom adopted the Unsentenced Kalman Filter (UKF) based approach which gives a good accuracy for SOC estimation.

Unsentenced Kalman Filter (UKF) Approach: It is an adaptive model approach which is highly accurate and precise. Unscented Kalman Filter was proposed by Julier and Uhlman.

For state estimation first develop a battery model based on equivalent circuit modelling approach.

Equivalent Circuit Model (ECM):

Li-ion battery has a dynamic charge/discharge characteristics. ECM represents the charge discharge curve of the battery with the help of electrical components like resistors, capacitors and voltage source and form a circuit network.

Commonly used Equivalent Circuit Models

• Thevenin equivalent model
• • 1st, 2nd, 3rd RC models
• Impedance based model
• Hysteresis model
• • Zero-state, One-state models
• Enhanced Self Correcting (ESC) model
• • Two-state low pass filter, four-state low pass filter

Exicom adopted 2RC Thevenin equivalent circuit battery model which is shown in figure 3

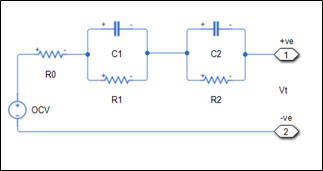
Where R0 represents the internal resistance of the battery, OCV (Open Circuit Voltage) is denoted by a voltage source and RC branches (R1C1 and R2C2) represent the dynamic response of battery. The dynamic response of the battery is due to polarization effect (active and concentration polarization)

Compactness: Accurate SOC and battery state information allows the battery pack to be used aggressively within the design limits

Reliability: A good SOC estimator is consistent and enhancing overall power-system reliability.

Economy: Warranty service on a reliable system costs less.

Exicom Role

R&D Exicom is aggressively working on SOX (SOC, SOH, SOP and SOE) algorithms with novel research.
For SOC estimation, Exicom adopted the Unsentenced Kalman Filter (UKF) based approach which gives a good accuracy for SOC estimation.

Unsentenced Kalman Filter (UKF) Approach: It is an adaptive model approach which is highly accurate and precise. Unscented Kalman Filter was proposed by Julier and Uhlman.

For state estimation first develop a battery model based on equivalent circuit modelling approach.

Equivalent Circuit Model (ECM):

Li-ion battery has a dynamic charge/discharge characteristics. ECM represents the charge discharge curve of the battery with the help of electrical components like resistors, capacitors and voltage source and form a circuit network.

Commonly used Equivalent Circuit Models

• Thevenin equivalent model
• • 1st, 2nd, 3rd RC models
• Impedance based model
• Hysteresis model
• • Zero-state, One-state models
• Enhanced Self Correcting (ESC) model
• • Two-state low pass filter, four-state low pass filter

Optimization: 2RC model parameters are optimized with experimental data using a pulse discharge or HPPC approach. For optimization Matlab optimization tool is used.

UKF applied with ECM

Kalman filter solves problems as two state estimation problem. Kalman Filter uses the propagation of a Gaussian random variable (GRV) through the system dynamics.

In the Extended Kalman filter (EKF), the state transition is approximated by Gaussian random variables, which is then propagated analytically through the nonlinear system. This can introduce large errors in the posterior mean and covariance of the transformed Gaussian random variables, which may affect the performance of the filter. The UKF addresses this problem by using a deterministic sampling approach. The state transition is again approximated by Gaussian random variables, but is now represented using a set of carefully chosen sample points. These sample points completely capture the true mean and covariance of the Gaussian random variables, and name as sigma points.

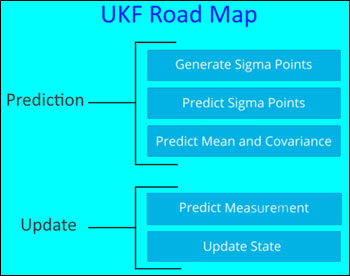
UKF Road Map

State Transition Equations

The state transition equation developed for the battery model is given below

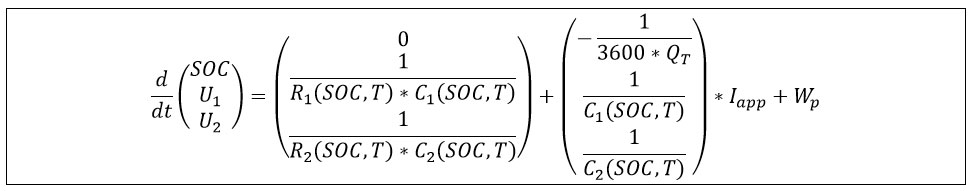
Where 〖R_1 C〗_1 and 〖R_2 C〗_2 and are the thermal and SOC dependent resistors and capacitors in the RC blocks, U_1,U_2 are the voltages across capacitors C_1 and C_2 respectively, I_app is the input current, T is the battery temperature, Q_T is the battery capacity (Ah), and W_p is the process noise.

The measurement equation is given as:

Where V_(t )is the output terminal voltage, R_0 is the internal resistance, OCV is the open circuit voltage, and N_m is the measurement noise.

Developed SOC model

First discretize the state equations using Euler discretization approach. The discretized state transition equation is implemented as a Matlab Simulink function (batteryStateFcn) to develop the complete UKF based SOC model.

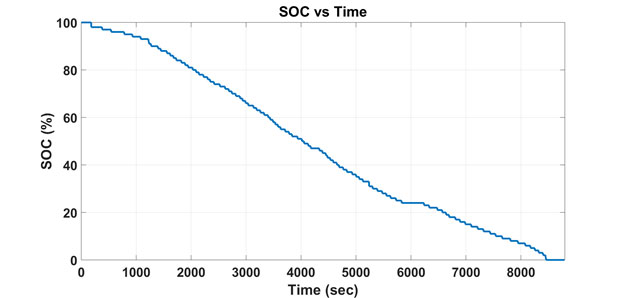
SOC Graph

Figure 6 shows the SOC of a battery pack during discharging.